
贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设:“如果一个袋子中共有 10 个球,分别是黑球和白球,但是我们不知道它们之间的比例是怎么样的,现在,仅通过摸出的球的颜色,是否能判断出袋子里面黑白球的比例?”
上述问题可能与我们高中时期所接受的的概率有所冲突,因为你所接触的概率问题可能是这样的:“一个袋子里面有 10 个球,其中 4 个黑球,6 个白球,如果你随机抓取一个球,那么是黑球的概率是多少?”毫无疑问,答案是 0.4。这个问题非常简单,因为我们事先知道了袋子里面黑球和白球的比例,所以很容易算出摸一个球的概率,但是在某些复杂情况下,我们无法得知“比例”,此时就引出了贝叶斯提出的问题。
在统计学中有两个较大的分支:一个是“频率”,另一个便是“贝叶斯”,它们都有各自庞大的知识体系,而“贝叶斯”主要利用了“相关性”一词。下面以通俗易懂的方式描述一下“贝叶斯定理”:通常,事件 A 在事件 B 发生的条件下与事件 B 在事件 A 发生的条件下,它们两者的概率并不相同,但是它们两者之间存在一定的相关性,并具有以下公式(称之为“贝叶斯公式”):
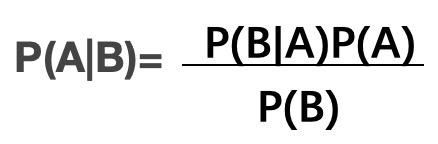
看到上述公式,你可能一头雾水,不过不必慌张,下面我们来了解一下“贝叶斯”公式。
符号意义
首先我们要了解上述公式中符号的意义:
P(A) 这是概率中最基本的符号,表示 A 出现的概率。比如在投掷骰(tóu)子【俗称“色(shǎi)子】时,P(2) 指的是骰子出现数字“2”的概率,这个概率是六分之一。
P(B|A) 是条件概率的符号,表示事件 A 发生的条件下,事件 B 发生的概率,条件概率是“贝叶斯公式”的关键所在,它也被称为“似然度”。
P(A|B) 是条件概率的符号,表示事件 B 发生的条件下,事件 A 发生的概率,这个计算结果也被称为“后验概率”。
有上述描述可知,贝叶斯公式可以预测事件发生的概率,两个本来相互独立的事件,发生了某种“相关性”,此时就可以通过“贝叶斯公式”实现预测。
条件概率
条件概率是“贝叶斯公式”的关键所在,那么如何理解条件概率呢?其实我们可以从“相关性”这一词语出发。举一个简单的例子,比如小明和小红是同班同学,他们各自准时回家的概率是 P(小明回家) = 1/2 和 P(小红回家) =1/2,但是假如小明和小红是好朋友,每天都会一起回家,那么 P(小红回家|小明回家) = 1 (理想状态下)。
上述示例就是条件概率的应用,小红和小明之间产生了某种关联性,本来俩个相互独立的事件,变得不再独立。但是还有一种情况,比如小亮每天准时到家 P(小亮回家) =1/2,但是小亮喜欢独来独往,如果问 P(小亮回家|小红回家) 的概率是多少呢?你会发现这两者之间不存在“相关性”,小红是否到家,不会影响小亮的概率结果,因此小亮准时到家的概率仍然是 1/2。
贝叶斯公式的核心是“条件概率”,譬如 P(B|A),就表示当 A 发生时,B 发生的概率,如果P(B|A)的值越大,说明一旦发生了A,B 就越可能发生。两者可能存在较高的相关性。
先验概率
在贝叶斯看来,世界并非静止不动的,而是动态和相对的,他希望利用已知经验来进行判断,那么如何用经验进行判断呢?这里就必须要提到“先验”和“后验”这两个词语。我们先讲解“先验”,其实“先验”就相当于“未卜先知”,在事情即将发生之前,做一个概率预判。比如从远处驶来了一辆车,是轿车的概率是 45%,是货车的概率是 35%,是大客车的概率是 20%,在你没有看清之前基本靠猜,此时,我们把这个概率就叫做“先验概率”。
后验概率
在理解了“先验概率”的基础上,我们来研究一下什么是“后验概率?”
我们知道每一个事物都有自己的特征,比如前面所说的轿车、货车、客车,它们都有着各自不同的特征,距离过远的时候,我们无法用肉眼分辨,而当距离达到一定范围内就可以根据各自的特征再次做出概率预判,这就是后验概率。比如轿车的速度相比于另外两者更快可以记做 P(轿车|速度快) = 55%,而客车体型可能更大,可以记做 P(客车|体型大) = 35%。
如果用条件概率来表述 P(体型大|客车)=35%,这种通过“车辆类别”推算出“类别特征”发生的的概率的方法叫作“似然度”。这里的似然就是“可能性”的意思。
托马斯•贝叶斯
贝叶斯(1701年—1761年,Thomas Bayes),英国数学家。1701年出生于伦敦,做过神父。1742年成为英国皇家学会会员。1761年4月7日逝世。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论,并创立了贝叶斯统计理论,对于统计决策函数、统计推断、统计的估算等做出了贡献。1763年由Richard Price整理发表了贝叶斯的成果《An Essay towards solving a Problem in the Doctrine of Chances》,对于现代概率论和数理统计都有很重要的作用。贝叶斯的另一著作《机会的学说概论》发表于1758年。贝叶斯所采用的许多术语被沿用至2021。
内容来源:
http://c.biancheng.net/ml_alg/bayes-theorem.html
通俗地理解贝叶斯公式(定理)
摘自:《解决问题教程》(第二版,许湘岳、吴强等主编,人民出版社)
来源:教育部高校毕业生就业协会核心能力分会
主办:CVCC职业核心能力认证办公室
协办:北京桑博国际教育科技有限公司
邮箱:cvcc@cvcc.net.cn
微信:cvcc2006
电话:010-84824728
博客:http://blog.sina.com.cn/cvcc2006
